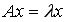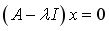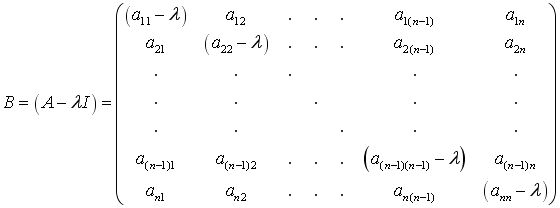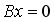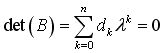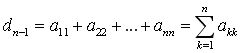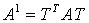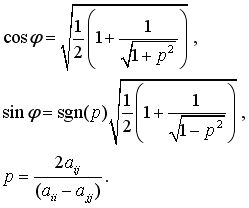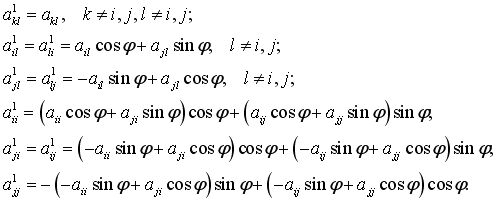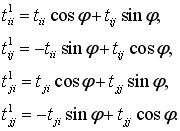|
| 0. Содержание |
|
|
|
| 1. Постановка |
|
| На самом деле никакой проблемы уже нет. Эти задачи решены разными математиками в разное время и много раз. Но прежде, чем рассказывать о методах решения (точнее, здесь пойдет речь об одном методе – методе вращений, предложенным Якоби) нужно рассказать о самой задаче. |
| Потом я напишу две версии программы. Одну не оптимизированную, другую оптимизированную. А в качестве программного средства буду использовать MS Excel и VBA. |
| Вы удивлены? Готов дать необходимые разъяснения по этому поводу. |
| MS Excel хорош тем, что позволяет скромными средствами добиться приятного внешнего вида. Я приведу обе программы полностью и в коде выделю курсивом, части относящиеся к красивизму, а не к алгоритму. Вы убедитесь, что это совсем немного. |
Итак, число 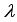 называется собственным значением матрицы называется собственным значением матрицы 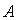 , если существует не нулевой вектор , если существует не нулевой вектор 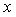 , такой что , такой что |
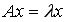 |
(1.1) |
|
При этом вектор 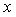 называется собственным вектором матрицы называется собственным вектором матрицы 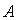 . . |
| Выражение (1.1) можно переписать так: |
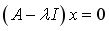 |
(1.2) |
|
Здесь 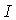 - единичная матрица. - единичная матрица. |
| Выражение в скобках определяет матрицу: |
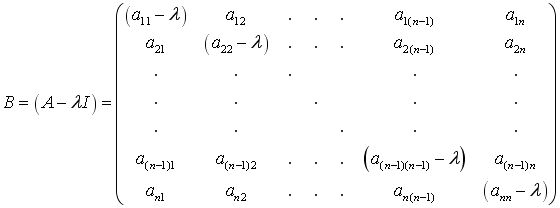 |
(1.3) |
|
| То есть, мы получили матричное уравнение: |
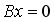 |
(1.4) |
|
| В выражениях (1.2) и (1.4) под нулем в правой части понимается нуль-вектор. |
| Матричное уравнение (1.4) представляет собой систему линейных однородных уравнений. Оно имеет решение, если главный определитель равен нулю: |
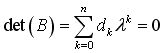 |
(1.5) |
|
Когда мы решим это уравнение, получим n значений 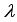 . Это и будут собственные значения. Для каждого . Это и будут собственные значения. Для каждого 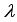 составим матрицу (1.3) и решим уравнение (1.4). В конце концов, получим n собственных векторов составим матрицу (1.3) и решим уравнение (1.4). В конце концов, получим n собственных векторов 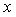 . . |
Вот здесь и возникли проблемы, о которых идет речь в названии статьи. Ведь для решения нужно составить уравнение (1.5) и решить его (что для больших порядков уже не просто). А потом еще и для каждого 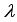 решить (1.4). То есть нужно решить n матричных уравнений. Задача получается достаточно объемной. решить (1.4). То есть нужно решить n матричных уравнений. Задача получается достаточно объемной. |
ПРИМЕЧАНИЕ 1.1: Коэффициенты 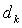 характеристического многочлена (1.5) оператора характеристического многочлена (1.5) оператора 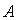 представляют собой инварианты относительно выбора базиса. В частности: представляют собой инварианты относительно выбора базиса. В частности: |
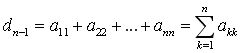 |
(1.6) |
|
| Это выражение называется следом и обозначается Sp. В литературе можно еще встретить обозначение tr. |
| А почему бы нам просто не сметить базис, таким образом, чтобы в новой матрице все элементы, кроме стоящих на главной диагонали, обнулились? Если нам это удастся сделать, то вектора задающие новый базис будут собственными векторами, а элементы стоящие на главных диагоналях – собственными значениями. |
|
| 2. Суть метода |
|
Якоби (математик XIX века) рассматривал вещественную симметричную матрицу 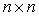 . Почему симметричную? Потому, что с несимметричными матрицами дело обстоит гораздо сложнее. К тому же, симметричные матрицы встречаются в приложениях гораздо чаще. Для перехода к новому базису, Якоби предложил следующее преобразование. . Почему симметричную? Потому, что с несимметричными матрицами дело обстоит гораздо сложнее. К тому же, симметричные матрицы встречаются в приложениях гораздо чаще. Для перехода к новому базису, Якоби предложил следующее преобразование. |
Построим матрицу 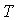 : : |
 |
(2.1) |
|
Возьмем теперь нашу матрицу 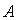 и выполним преобразование: и выполним преобразование: |
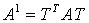 |
(2.2) |
|
Такое преобразование называется вращением (отсюда и название метода – метод вращений), а матрица 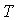 – матрицей вращения. – матрицей вращения. |
| Преобразования (2.2) обладают следующими свойствами: |
1. Сохраняют свойства симметрии: 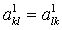 ; ; |
| 2. Изменяются только элементы, стоящие в i- ой и j- ой строке и в j- м и i- м столбце; |
| 3. Сохраняются собственные значения и собственные векторы. |
Суть метода Якоби заключается в алгоритме построения последовательности матриц вращения: 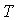 . Якоби предложил строить матрицу . Якоби предложил строить матрицу 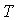 таким образом, чтобы после очередного вращения уничтожался максимальный недиагональный элемент. таким образом, чтобы после очередного вращения уничтожался максимальный недиагональный элемент. |
Чтобы построить эту матрицу 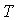 нужно ответить на два вопроса: нужно ответить на два вопроса: |
Во-первых, каково значение угла 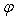 ? ? |
И, во-вторых, куда мы будем ставить 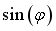 и и 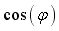 ? ? |
Ответ на второй вопрос дает свойство 2. Разумеется, 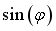 и и 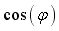 нужно ставить так, чтобы изменился максимальный недиагональный элемент нужно ставить так, чтобы изменился максимальный недиагональный элемент 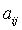 . . |
Для ответа на первый вопрос, придется проделать несколько преобразований (рекомендую это проделать самостоятельно). Главное помнить, что новый элемент 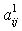 должен обнулиться. В итоге, получим следующие формулы: должен обнулиться. В итоге, получим следующие формулы: |
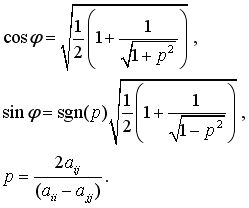 |
(2.3) |
|
| Несмотря, на то, что формулы страшные, преобразования действительно не сложные и под силу хорошему девятикласснику, если ему объяснить, как умножаются матрицы. |
Итак, после одного преобразования, мы получили новую матрицу 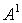 , у которой на месте максимального элемента матрицы , у которой на месте максимального элемента матрицы 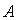 стоит 0. Самое главное, что при таком преобразовании сохранились собственные значения и вектора (см. свойство 3). А что делать дальше? Совершенно верно, произвести те же операции с новой матрицей стоит 0. Самое главное, что при таком преобразовании сохранились собственные значения и вектора (см. свойство 3). А что делать дальше? Совершенно верно, произвести те же операции с новой матрицей 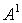 . Ищем максимальный элемент в матрице . Ищем максимальный элемент в матрице 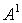 и уничтожаем его описанным выше способом. и уничтожаем его описанным выше способом. |
| “Вот и все”, - подумает торопливый читатель. – “Теперь, будем “убивать” элементы до тех пор, пока не получим диагональную матрицу”. Более вдумчивый читатель, может задать справедливый вопрос: “А “не воскреснет ли” элемент “убитый” ранее?” Что ж, приходится отвечать – Да, воскреснет. |
| Так что же, метод не работает? Всё впустую? |
Спешу вас успокоить, не всё впустую… Элемент, убитый на предыдущем шаге может возникнуть, но уже меньший по модулю! В книге [1] авторами доказывается сходимость данного метода. Доказательство основано, на том, что сумма квадратов недиагональных элементов матрицы 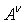 ( (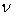 - номер шага) стремится к нулю. - номер шага) стремится к нулю. |
| Преобразования мы будем выполнять, до тех пор, пока максимальный недиагональный элемент по модулю не будет превышать указанной точности. |
| Настало время, когда можно перейти к программе. Нет смысла приводить здесь весь код программы, его можно скачать здесь. Я дам лишь небольшой комментарий. |
|
| 3. Первая программа |
|
| Переходим к реализации алгоритма. В модуле mdlMain находится несколько процедур и функция. Перечислю их: |
 Clear() - Процедура отчистки рабочей области. Вызывается из меню и из главной процедуры. К алгоритму никакого отношения не имеет; Clear() - Процедура отчистки рабочей области. Вызывается из меню и из главной процедуры. К алгоритму никакого отношения не имеет; |
 Show(Row As Long) - Процедура вывода матрицы на рабочий лист. Row параметр, номер строки откуда выводить. К алгоритму никакого отношения не имеет; Show(Row As Long) - Процедура вывода матрицы на рабочий лист. Row параметр, номер строки откуда выводить. К алгоритму никакого отношения не имеет; |
 MultMatrix(FirstMatr() As Double, SecondMatr() As Double, ResMatrix() As Double) - Процедура умножения матриц. FirstMatr() – первый массив, SecondMatr() – второй массив, ResMatrix() – результирующий массив. Все массивы размерности N на N; MultMatrix(FirstMatr() As Double, SecondMatr() As Double, ResMatrix() As Double) - Процедура умножения матриц. FirstMatr() – первый массив, SecondMatr() – второй массив, ResMatrix() – результирующий массив. Все массивы размерности N на N; |
 Transp(InputMatrix() As Double) - Процедура транспонирования матрицы. Входной параметр InputMatrix() – массив опять же размерности N на N; Transp(InputMatrix() As Double) - Процедура транспонирования матрицы. Входной параметр InputMatrix() – массив опять же размерности N на N; |
 Swap(A As Double, B As Double) - Процедура , меняющая значения две переменных A и B Swap(A As Double, B As Double) - Процедура , меняющая значения две переменных A и B |
 MyGenerate() - Процедура формирующая диагональную матрицу и вращающая ее произвольным образом. Результатом работы этой процедуры будет симметричная матрица; MyGenerate() - Процедура формирующая диагональную матрицу и вращающая ее произвольным образом. Результатом работы этой процедуры будет симметричная матрица; |
 Main() - Из названия видно, что это главная процедура. Здесь реализован алгоритм! Main() - Из названия видно, что это главная процедура. Здесь реализован алгоритм! |
 Sp() As Double - Функция вычисления следа матрицы. Напомню, след должен сохраняться (см. ПРИМЕЧАНИЕ 1.1) Sp() As Double - Функция вычисления следа матрицы. Напомню, след должен сохраняться (см. ПРИМЕЧАНИЕ 1.1) |
 Private Declare Sub Sleep Lib "kernel32" (ByVal dwMilliseconds As Long) - Это API-шная функция, используется для задержки выполнения. Private Declare Sub Sleep Lib "kernel32" (ByVal dwMilliseconds As Long) - Это API-шная функция, используется для задержки выполнения. |
| Сейчас перечислю константы и локальные переменные, описанные в модуле mdlMain. Для экономии места и слов приведу листинг. |
| Листинг 3.1 (Matrix01.xls!mdlMain) |
Private Const Epsilon As Double = 0.000001 ‘Задаем точность.
Private Const ShowMult As Boolean = True ‘Константа вывода.
‘True – как ”мультик”.
‘False просто вывод
‘в столбик.
Private Matrix() As Double ‘Исходная матрица, генерируется симметричной.
Private tmpMatrix() As Double ‘Поверьте, нам это понадобится
Private N As Long ‘Размерность матрицы
Private NewTMatrix() As Double ‘Тоже временный массив
Private TMatrix() As Double ‘В этом массиве получим ‘собственные вектора
Private Pi As Double ‘Из названия ясно, что это число Pi. 3.14 и т.д.
Private Row As Long |
|
| В Листинге 3.2 приведена часть процедуры Main. Полностью ее можно найти в файле Matrix01.xls. |
Листинг 3.2 (Matrix01.xls!mdlMain.Main) |
Do While (Amax >= Epsilon)
If Abs(Matrix(IMax, IMax) - Matrix(JMax, JMax)) > Epsilon Then
p = 2 * Matrix(IMax, JMax) / (Matrix(IMax, IMax) - Matrix(JMax, JMax))
CosFi = (0.5 * (1 + (1 + p ^ 2) ^ (-0.5))) ^ 0.5
SinFi = (Abs(p) / p) * (0.5 * (1 - (1 + p ^ 2) ^ (-0.5))) ^ 0.5
Else
CosFi = Cos(Pi / 2)
SinFi = Sin(Pi / 2)
End If
For I = 1 To N
For J = 1 To N
If I = J Then
TMatrix(I, J) = 1
Else
TMatrix(I, J) = 0
End If
Next J
Next I
TMatrix(IMax, IMax) = CosFi
TMatrix(IMax, JMax) = SinFi
TMatrix(JMax, IMax) = -SinFi
TMatrix(JMax, JMax) = CosFi
MultMatrix TMatrix, Matrix, tmpMatrix
Transp TMatrix
MultMatrix tmpMatrix, TMatrix, Matrix
MultMatrix TMatrix, NewTMatrix, tmpMatrix
For I = 1 To N
For J = 1 To N
NewTMatrix(I, J) = tmpMatrix(I, J)
Next J
Next I
pIMax = IMax
pJMax = JMax
Iter = Iter + 1
Amax = Matrix(1, 2) ^ 2
For I = 1 To N
For J = I + 1 To N
If Matrix(I, J) ^ 2 >= Amax Then
Amax = Matrix(I, J) ^ 2
IMax = I
JMax = J
End If
Next J
Next I
ActiveSheet.Range("A" + CStr(Row)).FormulaR1C1 = "Итерация номер " + CStr(Iter)
ActiveSheet.Range("C" + CStr(Row)).FormulaR1C1 = "Sp = "
ActiveSheet.Range("D" + CStr(Row)).Value = Sp
Show Row
Row = Row + N + 1
If ShowMult Then
Row = Row - N - 1
ActiveSheet.Cells(pIMax + Row, pJMax + 1).Interior.ColorIndex = 3
ActiveSheet.Cells(IMax + Row, JMax + 1).Interior.ColorIndex = 6
Sleep 300
ActiveSheet.Cells(pIMax + Row, pJMax + 1).Interior.ColorIndex = xlNone
ActiveSheet.Cells(IMax + Row, JMax + 1).Interior.ColorIndex = xlNone
End If
Loop |
|
|
| 4. Тестирование |
|
| И вот, мы запустили программу, сгенерировали симметричную матрицу. Посчитали собственные значения и собственные вектора. Но как проверить правильность результата? Для тестирования предлагаю следующее: |
| Создаем диагональную матрицу, случайным образом вращаем ее, а потом запускаем алгоритм диагонализации. Для этих целей написана процедура MyGenerate. Ниже привожу результат работы этой программе в отладочном режиме. |
| Таблица 4.1. Диагональная матрица, сформированная процедурой MyGenerate. |
| 20.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.0000 | 7.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.0000 | 0.0000 | 4.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.0000 | 0.0000 | 0.0000 | 10.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 18.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 17.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 19.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 13.0000 | 0.0000 | 0.0000 |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 11.0000 | 0.0000 |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.0000 |
|
| Таблица 4.2. Та же матрица после вращения. |
| 3.1023 | -3.2729 | 0.0495 | 0.5090 | -0.2170 | 0.0910 | 0.0696 | -0.1122 | -0.0765 | -0.0660 |
| -3.2729 | 11.7507 | -0.4360 | -2.0358 | 0.6198 | -0.4415 | -0.3166 | 0.3614 | 0.2269 | 0.1469 |
| 0.0495 | -0.4360 | 15.9497 | 0.3349 | -1.8158 | -0.3312 | 1.2856 | -0.5888 | 0.8250 | 5.4117 |
| 0.5090 | -2.0358 | 0.3349 | 15.3532 | -2.5468 | -0.2661 | 0.0977 | -1.0165 | -1.1691 | -2.8485 |
| -0.2170 | 0.6198 | -1.8158 | -2.5468 | 13.3606 | 0.5492 | 0.5568 | -1.1524 | 0.1573 | 0.9818 |
| 0.0910 | -0.4415 | -0.3312 | -0.2661 | 0.5492 | 13.1135 | -2.9265 | 0.8328 | 0.3857 | 2.0441 |
| 0.0696 | -0.3166 | 1.2856 | 0.0977 | 0.5568 | -2.9265 | 15.4399 | 0.4091 | 0.8888 | 0.3582 |
| -0.1122 | 0.3614 | -0.5888 | -1.0165 | -1.1524 | 0.8328 | 0.4091 | 16.1489 | 3.0594 | -2.5543 |
| -0.0765 | 0.2269 | 0.8250 | -1.1691 | 0.1573 | 0.3857 | 0.8888 | 3.0594 | 8.3253 | 0.1993 |
| -0.0660 | 0.1469 | 5.4117 | -2.8485 | 0.9818 | 2.0441 | 0.3582 | -2.5543 | 0.1993 | 8.4560 |
|
| Таблица 4.3. Матрица, представленная в Таблице 4.2, после диагонализации. На главной диагонали собственные значения. |
| 2.0000 | -0.0003 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| -0.0003 | 13.0000 | 0.0000 | 0.0000 | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0004 |
| 0.0000 | 0.0000 | 20.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | -0.0003 | -0.0009 | 0.0000 |
| 0.0000 | 0.0000 | 0.0000 | 19.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.0000 | 0.0001 | 0.0000 | 0.0000 | 10.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0001 | 0.0000 |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 11.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 17.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.0000 | 0.0000 | -0.0003 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 18.0000 | 0.0000 | 0.0002 |
| 0.0000 | 0.0000 | -0.0009 | 0.0000 | 0.0001 | 0.0000 | 0.0000 | 0.0000 | 7.0000 | 0.0000 |
| 0.0000 | 0.0004 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0002 | 0.0000 | 4.0000 |
|
| Таблица 4.4. Таблица собственных векторов матрицы предстваленой в Таблице 4.2. |
| 0.9514 | -0.3078 | -0.0023 | -0.0092 | -0.0034 | -0.0020 | 0.0088 | -0.0024 | 0.0016 | 0.0012 |
| 0.2170 | 0.6601 | 0.1013 | 0.0767 | -0.4357 | 0.4390 | -0.3010 | 0.1119 | 0.0424 | -0.1165 |
| 0.0045 | -0.0015 | 0.7746 | -0.0693 | 0.2521 | -0.1920 | -0.1841 | 0.3435 | -0.2155 | -0.3107 |
| 0.0846 | 0.2293 | -0.1322 | 0.6822 | 0.4406 | -0.2401 | -0.3518 | 0.0808 | 0.0919 | 0.2583 |
| -0.0168 | -0.0614 | -0.1536 | -0.2507 | 0.6297 | 0.5848 | -0.2834 | -0.1717 | 0.0587 | -0.2402 |
| -0.1926 | -0.6177 | 0.0586 | 0.4377 | -0.3059 | 0.4110 | -0.2611 | 0.2080 | -0.1108 | 0.0078 |
| 0.0427 | 0.1376 | -0.0235 | 0.0891 | 0.2434 | 0.3692 | 0.6071 | 0.5474 | -0.1887 | 0.2671 |
| -0.0137 | -0.0417 | -0.4149 | -0.4396 | -0.0538 | -0.2044 | -0.4427 | 0.5825 | -0.1606 | 0.1640 |
| -0.0327 | -0.0967 | 0.0707 | -0.0405 | -0.0033 | -0.0110 | 0.0663 | 0.3430 | 0.9213 | -0.1096 |
| -0.0142 | -0.0406 | 0.4094 | -0.2577 | 0.0133 | 0.1538 | -0.1850 | -0.1830 | 0.1321 | 0.8094 |
|
| При внимательном сравнении Таблицы 4.3 и Таблицы 4.1 вы можете заметить, что значения стоящие на главной диагонали совпадают, но почему-то переставлены произвольным образом. К сожалению, я никак не могу прокомментировать это факт. Переставлены и переставлены, никакого противоречия тут нет. Никто и не обещал, что матрицы будут совпадать один в один. Главное, что они удовлетворяют определению. |
| Что, думаете всё? Нет, еще не всё. В самом начале я обещал дать две программы. |
| “А зачем собственно? Все работает. Можно отдохнуть!” |
| Этот алгоритм можно оптимизировать. Он будет работать быстрее и требовать меньше памяти. |
| “Ну, это сейчас не важно. У меня четвертый пень, памяти пол гига! Что тут твои матрицы??? Подумаешь, будут они считаться 10 секунд или 5 секунд!!!” |
| Те, кто так считают, могут дальше не читать. Но приведу три возражения. |
| Во-первых, если вам придется делать расчет, который длится где-нибудь месяц, то преимущество в 50% будет заметно. Согласитесь, один месяц и две недели – есть разница! |
| Во-вторых, при работе со специальным оборудованием (пример: телефон, установка какая-нибудь) его параметры могут не позволить вам так разбрасываться: мегабайт туда, мегабайт сюда. |
| И, наконец, в-третьих, хороший алгоритм это же красиво! |
|
| 5. Оптимизация |
|
| Так как матрица симметричная, то нет необходимости хранить ее полностью. Достаточно хранить только верхний или нижний треугольник (часть, матрицы лежащая выше или ниже главной диагонали, соответственно). Реализуем это следующим образом: создаем одномерный массив размеров K = ((1 + N) / 2) * N, где N – это размерность матрицы. Во всех местах, где мы обращаемся к элементам матрицы, будем вызывать специальную функцию GetIndex, которая по двум индексам квадратной матрицы будет давать нам индекс в одномерном массиве. |
| Такая оптимизация даст нам, например, для матрицы размер 20 на 20, следующие преимущества: |
Массив размером 20 на 20 типа Double, будет занимать в памяти 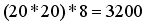 байтов, т.к. число типа Double занимает 8 байт. байтов, т.к. число типа Double занимает 8 байт. |
Массив размером 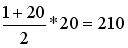 типа Double, будет отнимать 1680 байт. И так, мы сэкономили типа Double, будет отнимать 1680 байт. И так, мы сэкономили 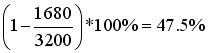 памяти. памяти. |
| Теперь подумаем, нужно ли выполнять полное умножение матриц при вращении? Так, как матрица (2.1) почти полностью состоит из 0, то нет смысла выполнять лишние операции. Все равно получится 0. Для вращения авторы [1] предлагают воспользоваться следующими преобразованиями: |
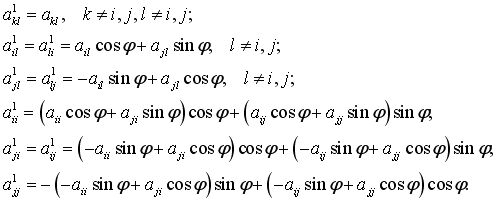 |
(5.1) |
|
| Точно по тем же причинам, нет необходимости при вычислении собственных векторов полностью умножать друг на друга матрицы. Я предлагаю использовать вот эти соотношения: |
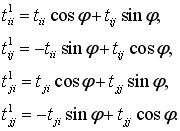 |
(5.2) |
|
| В Листинге 5.1 я приведу только часть оптимизированной процедуры Main. Полностью ее можно найти в файле Matrix02.xls. |
| Листинг 5.1 (Matrix02.xls!mdlMain.Main) |
Do While (Amax >= Epsilon)
If Abs(Matrix(GetIndex(IMax, IMax)) - Matrix(GetIndex(JMax, JMax))) > Epsilon Then
p = 2 * Matrix(GetIndex(IMax, JMax)) / _
(Matrix(GetIndex(IMax, IMax)) - Matrix(GetIndex(JMax, JMax)))
CosFi = (0.5 * (1 + (1 + p ^ 2) ^ (-0.5))) ^ 0.5
SinFi = (Abs(p) / p) * (0.5 * (1 - (1 + p ^ 2) ^ (-0.5))) ^ 0.5
Else
CosFi = Cos(Pi / 2)
SinFi = Sin(Pi / 2)
End If
For I = 1 To K
NewMatrix(I) = Matrix(I)
Next I
'Выполняем вращение согласно формулам (7)
For L = 1 To N
If (L <> IMax) And (L <> JMax) Then
NewMatrix(GetIndex(IMax, L)) = _
Matrix(GetIndex(IMax, L)) * CosFi + Matrix(GetIndex(JMax, L)) * SinFi
NewMatrix(GetIndex(JMax, L)) =
-Matrix(GetIndex(IMax, L)) * SinFi + Matrix(GetIndex(JMax, L)) * CosFi
End If
Next L
NewMatrix(GetIndex(IMax, IMax)) = _
(Matrix(GetIndex(IMax, IMax)) * CosFi + Matrix(GetIndex(JMax, IMax)) * SinFi) * CosFi + _
(Matrix(GetIndex(IMax, JMax)) * CosFi + Matrix(GetIndex(JMax, JMax)) * SinFi) * SinFi
NewMatrix(GetIndex(JMax, IMax)) = _
(-Matrix(GetIndex(IMax, IMax)) * SinFi + Matrix(GetIndex(JMax, IMax)) * CosFi) * CosFi + _
(-Matrix(GetIndex(IMax, JMax)) * SinFi + Matrix(GetIndex(JMax, JMax)) * CosFi) * SinFi
NewMatrix(GetIndex(JMax, JMax)) =
-(-Matrix(GetIndex(IMax, IMax)) * SinFi + Matrix(GetIndex(JMax, IMax)) * CosFi) * SinFi + _
(-Matrix(GetIndex(IMax, JMax)) * SinFi + Matrix(GetIndex(JMax, JMax)) * CosFi) * CosFi
‘Выполняем умножение матриц вращения согласно формулам (8)
Tii = TMatrix(IMax, IMax) * CosFi + TMatrix(IMax, JMax) * SinFi
Tij = -TMatrix(IMax, IMax) * SinFi + TMatrix(IMax, JMax) * CosFi
Tji = TMatrix(JMax, IMax) * CosFi + TMatrix(JMax, JMax) * SinFi
Tjj = -TMatrix(JMax, IMax) * SinFi + TMatrix(JMax, JMax) * CosFi
TMatrix(IMax, IMax) = Tii
TMatrix(IMax, JMax) = Tij
TMatrix(JMax, IMax) = Tji
TMatrix(JMax, JMax) = Tjj
For I = 1 To K
Matrix(I) = NewMatrix(I)
Next I
pIMax = IMax
pJMax = JMax
‘Ищем максимальный элемент
Iter = Iter + 1
Amax = Matrix(GetIndex(1, 2)) ^ 2
For I = 1 To N
For J = I + 1 To N
If Matrix(GetIndex(I, J)) ^ 2 >= Amax Then
Amax = Matrix(GetIndex(I, J)) ^ 2
IMax = I
JMax = J
End If
Next J
Next I
ActiveSheet.Range("A" + CStr(Row)).FormulaR1C1 = "Итерация номер " + CStr(Iter)
ActiveSheet.Range("C" + CStr(Row)).FormulaR1C1 = "Sp = "
ActiveSheet.Range("D" + CStr(Row)).Value = Sp
Show Row
Row = Row + N + 1
If ShowMult Then
Row = Row - N - 1
ActiveSheet.Cells(pIMax + Row, pJMax + 1).Interior.ColorIndex = 3
ActiveSheet.Cells(IMax + Row, JMax + 1).Interior.ColorIndex = 6
Sleep 300
ActiveSheet.Cells(pIMax + Row, pJMax + 1).Interior.ColorIndex = xlNone
ActiveSheet.Cells(IMax + Row, JMax + 1).Interior.ColorIndex = xlNone
End If
Loop |
|
Теперь оценим, сколько операторов мы будем выполнять за одну итерацию для матрицы размером 20 на 20 (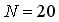 ). ). |
| В первом случае: |
 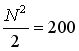 на поиск максимального значения по модулю среди недиагональных; на поиск максимального значения по модулю среди недиагональных; |
 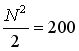 на генерацию единичной матрицы; на генерацию единичной матрицы; |
 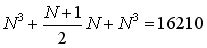 на один акт вращения; на один акт вращения; |
 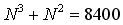 на вычисление собственных векторов. на вычисление собственных векторов. |
| В итоге получаем 25010 операторов выполняются за одну итерацию. |
| Во второй реализации: |
 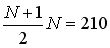 на поиск максимального значения по модулю среди недиагональных; на поиск максимального значения по модулю среди недиагональных; |
 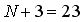 на один акт вращения; на один акт вращения; |
 8 на вычисление собственных векторов; 8 на вычисление собственных векторов; |
 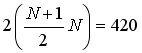 дополнительные операции. дополнительные операции. |
| Получаем 661 оператор за одну итерацию. Впечатляет? Почти в 40 раз меньше! Нужен ли еще какой-нибудь комментарий? |
|
| 6. Заключение |
|
| Осталась одна недосказанность. А откуда будет вызывать главная процедура Main? |
| Процедура создания меню AddMenu вызывается когда пользователь открывает нашу рабочую книгу или в том случае, когда пользователь переключается от одной открытой рабочей книги к нашей. Вызов осуществляется в обработчике события Workbook_Activate(). В нашем меню (оно называется Matrix) будет два элемента: |
| Первый элемент Generate. При нажатии выполняется процедура Main. |
| Второй – Clear. Вызывается процедура Clear – очистка рабочей области. |
| Процедура удаления меню DelMenu вызывается из обработчика Workbook_Deactivate() когда пользователь покидает нашу книгу. |
| Вот теперь все. Присылайте мне ваши замечания и рекомендации сюда. |
|
| 7. Список литературы |
|
| [1] Ильин В.А., Позняк Э.Г. Линейная алгебра М.: 1974, «Наука», 292 c. |
| |
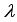 называется собственным значением матрицы
называется собственным значением матрицы 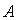 , если существует не нулевой вектор
, если существует не нулевой вектор 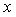 , такой что
, такой что 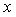 называется собственным вектором матрицы
называется собственным вектором матрицы 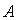 .
.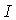 - единичная матрица.
- единичная матрица.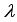 . Это и будут собственные значения. Для каждого
. Это и будут собственные значения. Для каждого 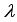 составим матрицу (1.3) и решим уравнение (1.4). В конце концов, получим n собственных векторов
составим матрицу (1.3) и решим уравнение (1.4). В конце концов, получим n собственных векторов 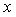 .
.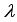 решить (1.4). То есть нужно решить n матричных уравнений. Задача получается достаточно объемной.
решить (1.4). То есть нужно решить n матричных уравнений. Задача получается достаточно объемной.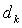 характеристического многочлена (1.5) оператора
характеристического многочлена (1.5) оператора 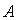 представляют собой инварианты относительно выбора базиса. В частности:
представляют собой инварианты относительно выбора базиса. В частности: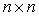 . Почему симметричную? Потому, что с несимметричными матрицами дело обстоит гораздо сложнее. К тому же, симметричные матрицы встречаются в приложениях гораздо чаще. Для перехода к новому базису, Якоби предложил следующее преобразование.
. Почему симметричную? Потому, что с несимметричными матрицами дело обстоит гораздо сложнее. К тому же, симметричные матрицы встречаются в приложениях гораздо чаще. Для перехода к новому базису, Якоби предложил следующее преобразование.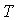 :
: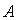 и выполним преобразование:
и выполним преобразование: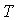 – матрицей вращения.
– матрицей вращения.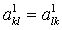 ;
;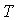 . Якоби предложил строить матрицу
. Якоби предложил строить матрицу 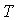 таким образом, чтобы после очередного вращения уничтожался максимальный недиагональный элемент.
таким образом, чтобы после очередного вращения уничтожался максимальный недиагональный элемент.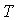 нужно ответить на два вопроса:
нужно ответить на два вопроса: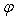 ?
?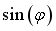 и
и 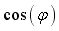 ?
?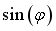 и
и 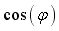 нужно ставить так, чтобы изменился максимальный недиагональный элемент
нужно ставить так, чтобы изменился максимальный недиагональный элемент 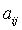 .
.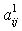 должен обнулиться. В итоге, получим следующие формулы:
должен обнулиться. В итоге, получим следующие формулы: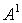 , у которой на месте максимального элемента матрицы
, у которой на месте максимального элемента матрицы 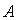 стоит 0. Самое главное, что при таком преобразовании сохранились собственные значения и вектора (см. свойство 3). А что делать дальше? Совершенно верно, произвести те же операции с новой матрицей
стоит 0. Самое главное, что при таком преобразовании сохранились собственные значения и вектора (см. свойство 3). А что делать дальше? Совершенно верно, произвести те же операции с новой матрицей 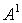 . Ищем максимальный элемент в матрице
. Ищем максимальный элемент в матрице 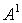 и уничтожаем его описанным выше способом.
и уничтожаем его описанным выше способом.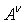 (
(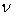 - номер шага) стремится к нулю.
- номер шага) стремится к нулю. Clear() - Процедура отчистки рабочей области. Вызывается из меню и из главной процедуры. К алгоритму никакого отношения не имеет;
Clear() - Процедура отчистки рабочей области. Вызывается из меню и из главной процедуры. К алгоритму никакого отношения не имеет; Show(Row As Long) - Процедура вывода матрицы на рабочий лист. Row параметр, номер строки откуда выводить. К алгоритму никакого отношения не имеет;
Show(Row As Long) - Процедура вывода матрицы на рабочий лист. Row параметр, номер строки откуда выводить. К алгоритму никакого отношения не имеет; MultMatrix(FirstMatr() As Double, SecondMatr() As Double, ResMatrix() As Double) - Процедура умножения матриц. FirstMatr() – первый массив, SecondMatr() – второй массив, ResMatrix() – результирующий массив. Все массивы размерности N на N;
MultMatrix(FirstMatr() As Double, SecondMatr() As Double, ResMatrix() As Double) - Процедура умножения матриц. FirstMatr() – первый массив, SecondMatr() – второй массив, ResMatrix() – результирующий массив. Все массивы размерности N на N; Transp(InputMatrix() As Double) - Процедура транспонирования матрицы. Входной параметр InputMatrix() – массив опять же размерности N на N;
Transp(InputMatrix() As Double) - Процедура транспонирования матрицы. Входной параметр InputMatrix() – массив опять же размерности N на N; Swap(A As Double, B As Double) - Процедура , меняющая значения две переменных A и B
Swap(A As Double, B As Double) - Процедура , меняющая значения две переменных A и B MyGenerate() - Процедура формирующая диагональную матрицу и вращающая ее произвольным образом. Результатом работы этой процедуры будет симметричная матрица;
MyGenerate() - Процедура формирующая диагональную матрицу и вращающая ее произвольным образом. Результатом работы этой процедуры будет симметричная матрица; Main() - Из названия видно, что это главная процедура. Здесь реализован алгоритм!
Main() - Из названия видно, что это главная процедура. Здесь реализован алгоритм! Sp() As Double - Функция вычисления следа матрицы. Напомню, след должен сохраняться (см. ПРИМЕЧАНИЕ 1.1)
Sp() As Double - Функция вычисления следа матрицы. Напомню, след должен сохраняться (см. ПРИМЕЧАНИЕ 1.1) Private Declare Sub Sleep Lib "kernel32" (ByVal dwMilliseconds As Long) - Это API-шная функция, используется для задержки выполнения.
Private Declare Sub Sleep Lib "kernel32" (ByVal dwMilliseconds As Long) - Это API-шная функция, используется для задержки выполнения.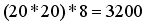 байтов, т.к. число типа Double занимает 8 байт.
байтов, т.к. число типа Double занимает 8 байт.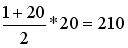 типа Double, будет отнимать 1680 байт. И так, мы сэкономили
типа Double, будет отнимать 1680 байт. И так, мы сэкономили 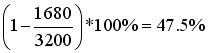 памяти.
памяти.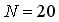 ).
).
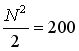 на поиск максимального значения по модулю среди недиагональных;
на поиск максимального значения по модулю среди недиагональных;
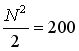 на генерацию единичной матрицы;
на генерацию единичной матрицы;
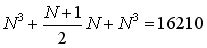 на один акт вращения;
на один акт вращения;
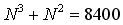 на вычисление собственных векторов.
на вычисление собственных векторов.
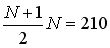 на поиск максимального значения по модулю среди недиагональных;
на поиск максимального значения по модулю среди недиагональных;
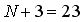 на один акт вращения;
на один акт вращения; 8 на вычисление собственных векторов;
8 на вычисление собственных векторов;
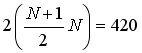 дополнительные операции.
дополнительные операции.